  II. Suppose that the population relationship between wage and years of education is 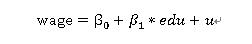 where wage represents the hourly wage rate, edu represents years of education and u is the population disturbance term.
Interpret the population parameters β_0 and β_1
β_0is the wage intercept for the population, which represents the mean value of the hourly wage rate(wage)when years of education is zero (edu=0).
β_1is the slope for the population, which represents the expected changes in hourly wage rate (wage)per unit change in years of education (edu). In other words, β_1 represents the mean amount that hourly wage rate (wage) changes for a one-unit change in years of education (edu).
Use the SLRM assumptions to show that the OLS β ̂_0 is an unbiased estimator for β_0.
 
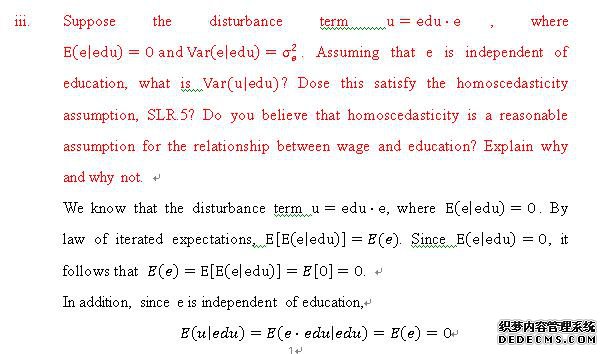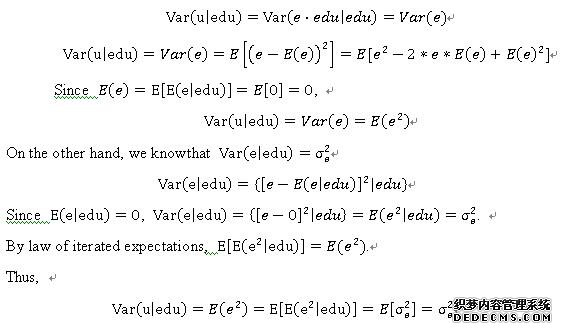
The homoscedasticity assumption, SLR.5 shows that the variance of the errors is constant for allvalues of X. For above proof, for all values of edu, the variance of the errors is equal to σ_e^2. Thus, this satisfies the homoscedasticity assumption, SLR.5.
In addition, I believe the homoscedasticityis a reasonable assumption for the relationship between wage and education. If the variance of the errors is not constant, the cases with larger disturbances have more “pull” than other observations, which will affect the accuracy of the regression model.
  
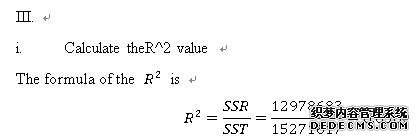
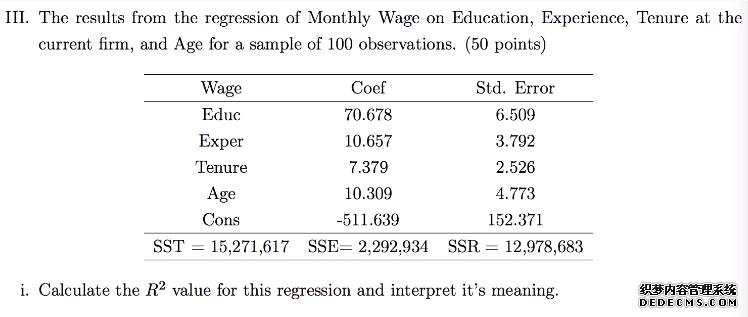
This implies 85.0% of the variation in wage is explained by the set of independent variables included in the regression model. In other words, 85.0% of the variability of wage has been accounted by predictors.
The null hypothesis is the marginal effect of an additional years of education is equal to $50. The alternative is the marginal effect of an additional years of education is greater than $50. The significance level is α=0.05. The formula of themarginal effect is
Because this interval does not includezero, we can conclude that there is a significant linear relationship between years of education and wage.
The null hypothesis is the marginal effect of an additional year of experience with the same fame is equal to $25. The alternative is the marginal effect of an additional year of experience with the same fame is different from $25. The significance level is α=0.05. The formula of themarginal effect is
  |
 |
|||
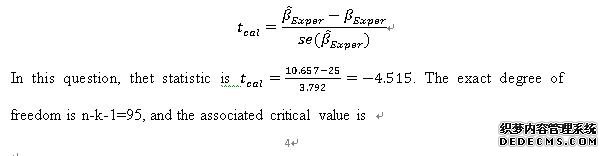| 网站地图 |
